How to Measure the Business Impact of LLMs

Table of Links

Abstract and 1. Introduction

2. Basic premises for our models

   2.1. How LLMs are charged

   2.2 An anedotal model from industry

   2.3 Choice of Costs in the Model

   2.4 Why multiple scenarios

3. A Decision Theoretic Model

   3.1 How to model success

4. A Model for Commercial Operations Based on a Single Transaction

   4.1 Example of Using the Model

   4.2 Model Analysis

   4.3 Discussion of the RoI vs. Earning dillema

5. Modelling of a Binary Classification Problem

   5.1 Local Sensitivity Analysis

   5.2 Global Sensitivity Analysis by Sobol Method

6. Related Work

7. Future work

8. Conclusion, References, and Acknowledgements

3 A Decision Theoretic Model

During the planning of a project, the earnings and RoI can only be estimated, as there are uncertainties and risks in projects [Project Management Institute, 2021]. Therefore, any decision should take these estimates into account. Therefore, we now model the expected value of earnings and RoI, E[E] and E[R] [Frahm, 2019].

Moreover, to allow for a better decision in theoretical and practical perspectives, one needs to establish a model that includes costs, gains, and losses from the use of an LLM and also a probabilistic view of success. In a decision-theoretic approach, this is possible, among other ways, by using Savage’s Theory of Rational Choice [Savage, 1954], as described by Frahm [2019].

According Savage’s theory, the expected value for the utility of an state s is:

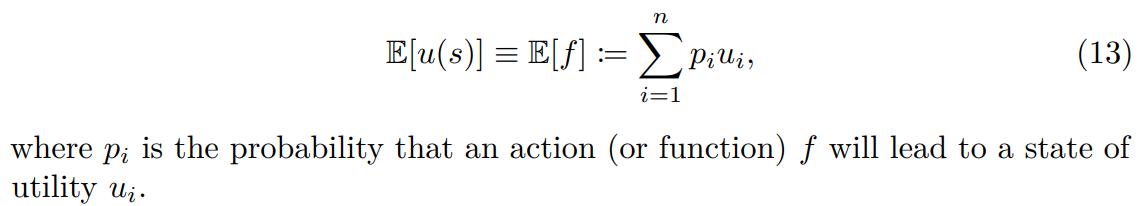
We start by considering the action of using an LLM to solve a business problem or improve a business situation, with only two possible outcomes, or states: success of failure of a business transaction. We initially model the probability of success as P and the probability of failure as (1 − P). Therefore the expected value (in earnings) and expected RoI of a project:

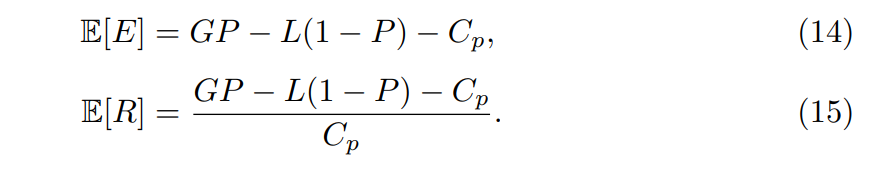
These decision-theoretic equations 14 and 15 will guide this article. For each proposed model, we will discuss how the variables G, L, P and Cp, in the form of cost per token C, affect E and R.

3.1 How to model success

In this work, we start by using the probability of success of an LLM in a business task as P. However, the analysis of such probability is not simple, due to the fact that there are actually two probabilities involved: the probability of an LLM to fulfill its task and the probability of the task having an effect on the business. For example, even if an LLM detects that users are prone to include a product in their basket, and a sales system on the Internet provides this suggestion to the users, they can decide not to or they be distracted by the offer and do not close the operation, resulting in a loss.

In this paper, we consider both probabilities as aggregated probabilities. However, we draw attention to the fact that the second probability is conditional to the first. Therefore, being Pb the probability of business success and Pt the probability of the specific LLM task success, one could have the basic assumption that:

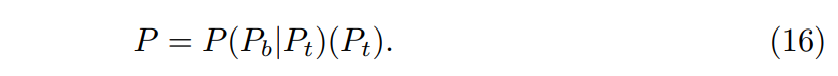
Moreover, a more realistic model should include the chance of business success when the LLM task fails. For example, it is possible that the LLM suggests a wrong product and, by chance, the customer accepts it. This can be modeled as:

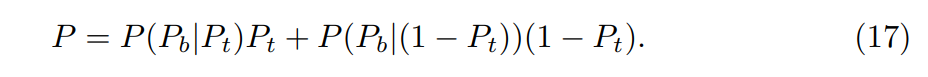
Finally, one can also model the probability of a correct prediction from the LLM to lead the user to a path where he does not complete the transaction. In this case, one should also model the probability of losing the transaction. We do that in section 5.