Intuitions Behind Multi-Token Prediction: Information Theory & Choice Points

Table of Links

Abstract and 1. Introduction

2. Method

3. Experiments on real data

3.1. Benefits scale with model size and 3.2. Faster inference

3.3. Learning global patterns with multi-byte prediction and 3.4. Searching for the optimal n

3.5. Training for multiple epochs and 3.6. Finetuning multi-token predictors

3.7. Multi-token prediction on natural language

4. Ablations on synthetic data and 4.1. Induction capability

4.2. Algorithmic reasoning

5. Why does it work? Some speculation and 5.1. Lookahead reinforces choice points

5.2. Information-theoretic argument

6. Related work

7. Conclusion, Impact statement, Environmental impact, Acknowledgements, and References

A. Additional results on self-speculative decoding

B. Alternative architectures

C. Training speeds

D. Finetuning

E. Additional results on model scaling behavior

F. Details on CodeContests finetuning

G. Additional results on natural language benchmarks

H. Additional results on abstractive text summarization

I. Additional results on mathematical reasoning in natural language

J. Additional results on induction learning

K. Additional results on algorithmic reasoning

L. Additional intuitions on multi-token prediction

M. Training hyperparameters

L. Additional intuitions on multi-token prediction

L.1. Comparison to scheduled sampling

In Section 5.2, we argued that multi-token prediction reduces the distribution mismatch between teacher-forced training and autoregressive evaluation of language models. Scheduled sampling (Bengio et al., 2015) is a curriculum learning method that likewise aims to bridge this gap in sequence prediction tasks by gradually replacing more and more input tokens with model-generated ones.

While effective in areas such as time series forecasting, scheduled sampling is, in our opinion, inapplicable to language modelling due to the discrete nature of text. Replacing ground truth input sequences by interleaving of ground truth and model-generated tokens frequently results in ungrammatical, factually wrong or otherwise incoherent text, which should be avoided at all cost. Moreover, unlike multi-token prediction, the technique originally developed for recurrent neural networks cannot easily be adapted for parallel training setups like the ones of transformer models.

L.2. Information-theoretic argument

We give details on the information-theoretic terms appearing in the decomposition in Section 5.2 and derive a relative version that similarly allows to decompose multi-token prediction losses. As in Section 5.2, denote by X the next token and by Y the second-next one, and omit conditioning on the preceding context C for ease of notation. In Section 5.2, we decomposed H(X) + H(Y )—the quantity of interest for 2-token prediction models—as follows:

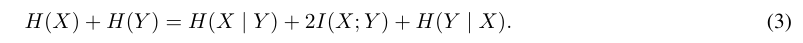
Let us explain each of the terms. The entropy terms denote the uncertainty contained in the ground-truth random variables X and Y. [2] The term H (Y | X) is a classical next-token entropy for the prefix (C, X). The conditional entropy H (X | Y) is a more theoretical entity not modelled by causal models. It describes the uncertainty about X given the prefix C and suffix Y, and therefore captures the local variations of X that do not affect the continuation of the text Y. The mutual information I(X; Y) on the other hand describes the information about Y contained in X (and vice versa) and therefore captures the variations of X which constrain the continuation of the text.

However, the argument given in Section 5.2 relies on the assumption that multi-token prediction losses obey a similar decomposition as the sum of the ground-truth entropies themselves. Let us make this rigorous. Denote by p(x, y) the joint distribution of X and Y , by p(x) (short for pX(x)) the marginal distribution of X and by p(y) the one of Y. Denote the densities of the model’s predictions by q(x, y), q(x) and q(y), respectively, conditional distributions by p (x | y) and Kullback-Leibler divergence from q to p by D(p ∥ q) and cross-entropy from q to p by H (p, q).

Definition L.1. The conditional cross-entropy H(pX|Y , qX|Y ) of X conditioned on Y from q to p is defined as the expectation under y of the cross-entropy between the distributions pX and qX conditioned on y, in formulas:

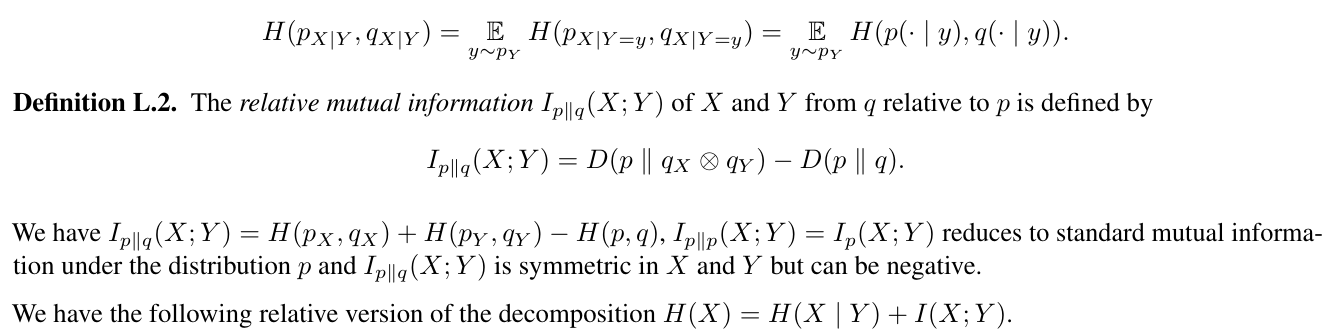
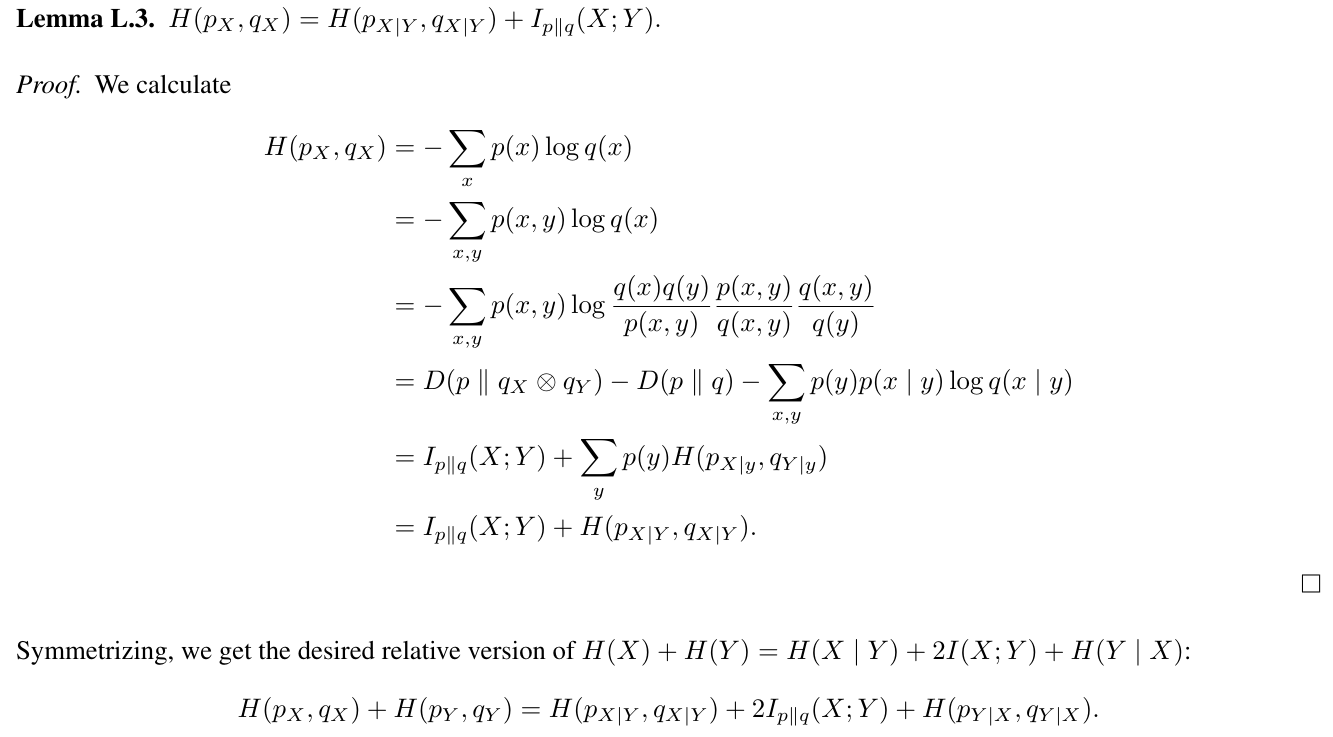
Setting p to be the empirical distribution of the training data, the left-hand side describes the cross-entropy loss used to train 2-token prediction models. The right-hand side gives the decomposition into a local cross-entropy term, a mutual information term with weight two and a shifted next-token cross-entropy term. We interpret this as follows: by adding the term H(pY , qY ) to the loss, 2-token prediction incentivizes models to precompute features which will become useful for predicting Y in the next step and increases the weight of the relative mutual information term in the loss. What does relative mutual information actually mean? By interpreting Kullback-Leibler divergence D(p ∥ q) as the average number of bits needed in addition to send data from p with a code optimized for q instead of p, we see that minimizing

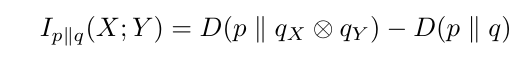
means minimizing the average number of additional bits needed to send data from p with a code optimized for q that treats X and Y as independent compared to one that does not. If this number is small, q managed to exploit the mutual information of X and Y under p.

L.3. Lookahead reinforces choice points

Training with multi-head prediction increases the importance of choice points in the loss in comparison to inconsequential decisions. To make this argument, we present a simplified model of language modelling. Consider a sequential decision task and a model M that is trained in a teacher-forced way on optimal trajectories. We distinguish choice points –transitions that lead to different outcomes – and inconsequential decisions which do not (Figure S17 (a) and (b)).

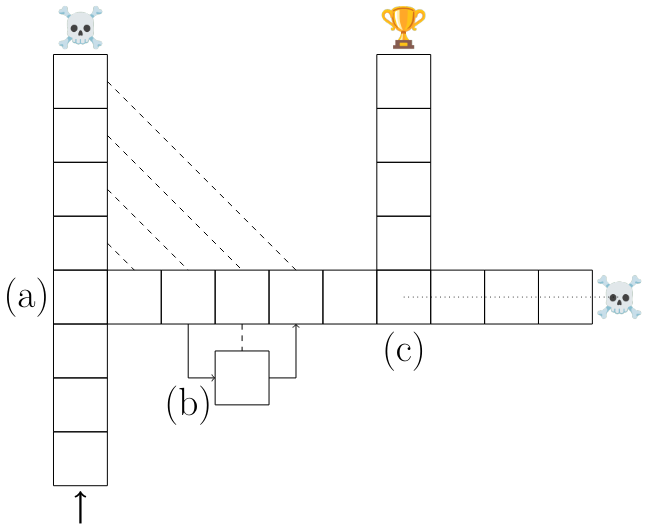
As argued in Section 5.1, we believe that this model captures important features of training and inference with language models: choice points are semantically important turning points in the generated texts, such as the final answer to a question or a specific line of code, while inconsequential decisions can be a choice among synonyms or of variable names in code.

L.4. Factorization orders

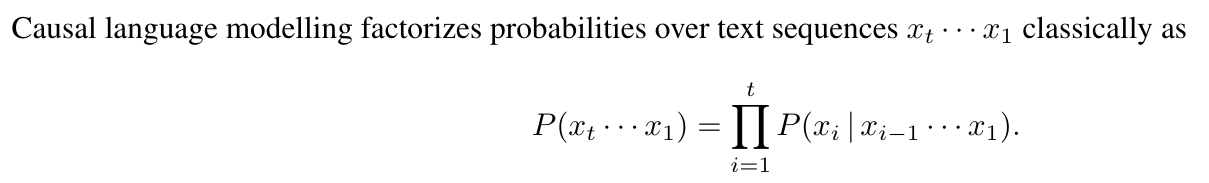
While moving forward in time is certainly the most natural choice of factorization order, there exist cases where it is suboptimal. In inflectional languages, for instance, agreement between related sentence parts is a frequent pattern with one word directing the grammatical forms of others. Consider the German sentence

Wie konnten auch Worte meiner durstenden Seele genügen?[3]

Friedrich Hölderlin, Fragment von Hyperion (1793)

where "genügen" requires a dative case object and then "Seele" requires the possessive pronoun "mein" to be in female singular dative form "meiner" and the participle "durstend" to be in female singular dative form in weak declination "durstenden" because it follows "meiner". In other words, the factorization order

Wie konnten auch Worte → genügen → Seele → meiner → durstenden?

is arguably an easier one for constructing the above sentence. Humans as well as language models therefore have to perform this factorization (which deviates from the causal order in which predictions take place!) within their latent activations, and a 4-token prediction loss makes this easier as it explicitly encourages models to have all information about the successive 4 tokens in its latent representations.

[2] In particular, they do not refer to model predictions.

[3] roughly: How could words be enough for my thirsty soul?